Прямая, заданная пересечением двух плоскостей. Линия пересечения плоскостей онлайн Линия пересечения двух плоскостей уравнение
Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и, то есть как множество точек, удовлетворяющих системе двух линейных уравнений
(V.5)
Справедливо
и обратное утверждение: система двух
независимых линейных уравнений вида
(V.5)
определяет прямую как линию пересечения
плоскостей (если они не параллельны).
Уравнения системы (V.5)
называются общим
уравнением
прямой
в пространстве
.
Пример V .12 . Составить каноническое уравнение прямой, заданной общими уравнениями плоскостей
Решение . Чтобы написать каноническое уравнение прямой или, что тоже самое, уравнение прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например Oyz и Oxz .
Точка
пересечения прямой с плоскостью Oyz
имеет абсциссу
.
Поэтому, полагая в данной системе
уравнений
,
получим систему с двумя переменными:
Ее
решение
,
вместе с
определяет точку
искомой прямой. Полагая в данной системе
уравнений
,
получим систему
решение
которой
,
вместе с
определяет точку
пересечения прямой с плоскостьюOxz
.
Теперь
запишем уравнения прямой, проходящей
через точки
и
:
или
,
где
будет направляющим векто-ром этой
прямой.
Пример
V
.13.
Прямая задана
каноническим уравнением
.
Составить общее уравнение этой прямой.
Решение. Каноническое уравнение прямой можно записать в виде системы двух независимых уравнений:
Получили
общее уравнение прямой, которая теперь
задана пересечением двух плоскостей,
одна из которых
параллельна осиOz
(
),
а другая
– осиОу
(
).
Данную прямую можно представить в виде линии пересечения двух других плоскостей, записав ее каноническое уравнение в виде другой пары независимых уравнений:
Замечание . Одна и та же прямая может быть задана различными системами двух линейных уравнений (то есть пересечением различных плоскостей, так как через одну прямую можно провести бесчисленное множество плоскостей), а также различными каноническими уравнениями (в зависимости от выбора точки на прямой и ее направляющего вектора).
Ненулевой вектор, параллельный прямой линии, будем называть ее направляющим вектором .
Пусть
в трехмерном пространстве
задана прямая l
,
проходящая через точку
,
и ее направляющий вектор
.
Любой
вектор
,
где
,
лежащий на прямой, коллинеарен с вектором
,
поэтому их координаты пропорциональны,
то есть
.
(V.6)
Это уравнение называется каноническим уравнением прямой. В частном случае, когда ﻉ есть плоскость, получаем уравнение прямой на плоскости
.
(V.7)
Пример
V
.14.
Найти уравнение прямой, проходящей
через две точки
,
.
,
где
,
,
.
Удобно уравнение (V.6) записать в параметрической форме. Так как координаты направляющих векторов параллельных прямых пропорциональны, то, полагая
,
где
t
– параметр,
.
Расстояние от точки до прямой
Рассмотри
двухмерное евклидовое пространство ﻉ
с
декартовой системой координат. Пусть
точка
ﻉ
и
l
ﻉ.
Найдем расстояние от этой точки до
прямой. Положим
,
и прямая l
задается уравнением
(рис.V.8).
Расстояние
,
вектор
,
где
– нормальный вектор прямой l
,
и
– коллинеарны, поэтому их координаты
пропорциональны, то есть
,
следовательно,
,
.
Отсюда
или умножая эти уравнения
наA
и B
соответственно и складывая их, находим
,
отсюда
.
(V.8)
определяет
расстояние от точки
до прямой
.
Пример
V
.15.
Найти уравнение прямой, проходящей
через точку
перпендикулярно прямойl
:
и найти расстояние от
до прямойl
.
Из
рис. V.8
имеем
,
а нормальный вектор прямойl
.
Из условия перпендикулярности имеем
Так
как
,
то
.
(V.9)
Это
и есть уравнение прямой, проходящей
через точку
,перпендикулярно
прямой
.
Пусть
имеем уравнение прямой (V.9),
проходящей через точку
,
перпендикулярна прямойl
:
.
Найдем расстояние от точки
до прямойl
,
используя формулу (V.8).
Для
нахождения искомого расстояния достаточно
найти уравнение прямой, проходящей
через две точки
и точку
,
лежащую на прямой в основании
перпендикуляра. Пусть
,
тогда
Так
как
,
а вектор
,
то
.
(V.11)
Поскольку
точка
лежит на прямойl
,
то имеем еще одно равенство
или
Приведем систему к виду, удобному для применения метода Крамера
Ее решение имеет вид
,
.
(V.12)
Подставляя (V.12) в (V.10), получаем исходное расстояние.
Пример
V
.16.
В двухмерном пространстве задана точка
и прямая
.
Найти расстояние от точки
до прямой; записать уравнение прямой,
проходящей через точку
перпендикулярно заданной прямой и найти
расстояние от точки
до основания перпендикуляра к исходной
прямой.
По формуле (V.8) имеем
Уравнение
прямой, содержащей перпендикуляр, найдем
как прямую, проходящую через две точки
и
,
воспользовавшись формулой (V.11).
Так как
,
то, с учетом того, что
,
а
,
имеем
.
Для
нахождения координат
имеем систему с учетом того, что точка
лежит на исходной прямой
Следовательно,
,
,
отсюда.
Рассмотрим
трехмерное евклидовое пространство ﻉ.
Пусть точка
ﻉ
и
плоскость ﻉ.
Найдем расстояние от этой точки
до плоскости,
заданной уравнением
(рис.V.9).
Аналогично
двухмерному пространству имеем
и вектор
,
а,
отсюда
.
(V.13)
Уравнение
прямой, содержащей перпендикуляр к
плоскости ,
запишем как уравнение прямой, проходящей
через две точки
и
,
лежащую в плоскости:
.
(V.14)
Для
нахождения координат точки
к двум любым равенствам формулы (V.14)
добавим уравнение
Решая
систему трех уравнений (V.14),
(V.15),
найдем
,
,
– координаты точки
.
Тогда уравнение перпендикуляра запишется
в виде
.
Для
нахождения расстояния от точки
до плоскости
вместо формулой (V.13)
воспользуемся
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:
Под углом
между двумя плоскостями будем понимать один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1
и α 2 равен одному из указанных смежных двугранных углов или 
. Поэтому 
. Т.к.
и 
, то
.
Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.
Условие параллельности двух плоскостей.
Две плоскости α 1 и α 2
параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит 
.
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
или
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .
Таким образом, .
Примеры.
ПРЯМАЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
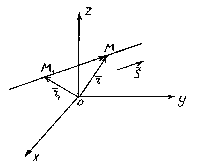
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .
Рассмотрим произвольную точку М(x,y,z)
на прямой. Из рисунка видно, что 
.
Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.
Запишем это уравнение в координатной форме.
Заметим, что ,
и отсюда
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
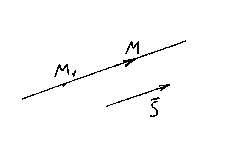
Пусть М
1 (x
1 , y
1 , z
1) – точка,
лежащая на прямой l
, и 
–
её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z)
и рассмотрим вектор .
Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,
– канонические
уравнения прямой.
Замечание 1.
Заметим, что канонические
уравнения прямой можно было получить из параметрических,исключив параметр t
. Действительно, из параметрических уравнений получаем 
или .
Пример.
Записать уравнение прямой 
в параметрическом виде.
Обозначим 
,
отсюда x
= 2 + 3t
, y
= –1 + 2t
, z
= 1 –t
.
Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид
Исключая из уравнений параметр t , получим уравнения прямой в виде
Однако и в этом случае условимся формально
записывать канонические уравнения прямой в виде
.
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает, что прямая
перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям 
соответствует прямая перпендикулярная осям Ox
и Oy
или параллельная оси Oz
.
Примеры.
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
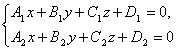
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
Построить прямую, заданную уравнениями 
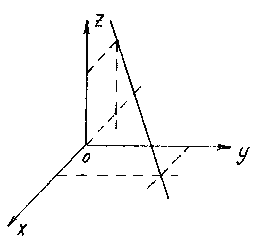
Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:
Решив эту систему, найдем точку M 1 (1;2;0).
Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :
От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.
Координаты точки
М
1
получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания
направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к
обоим нормальным векторам 
и 
.
Поэтому за направляющий вектор прямой l
можно взять векторное произведение нормальных векторов:
.
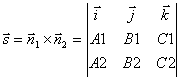Пример.
Привести общие уравнения прямой
к каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:
Нормальные векторы
плоскостей, определяющих прямую имеют координаты 
Поэтому направляющий вектор
прямой будет
.
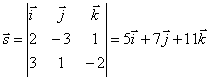Следовательно, l
: 
.
УГОЛ МЕЖДУ ПРЯМЫМИ
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим
Канонические уравнения прямой
Постановка задачи. Найти канонические уравнения прямой, заданной как линия пересечения двух плоскостей (общими уравнениями)
План решения.
Канонические уравнения прямой с направляющим вектором 
, проходящей через данную точку 
, имеют вид
. (1)
Поэтому, чтобы написать канонические уравнения прямой, необходимо найти ее направляющий вектор и какую-нибудь точку на прямой.
1. Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей, т.е. согласно определению векторного произведения, имеем
. (2)
2. Выбираем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой не параллелен хотя бы одной из координатных плоскостей, то прямая пересекает эту координатную плоскость. Следовательно, в качестве точки на прямой может быть взята точка ее пересечения с этой координатной плоскостью.
3. Подставляем найденные координаты направляющего вектора и точки в канонические уравнения прямой (1).
Замечание. Если векторное произведение (2) равно нулю, то плоскости не пересекаются (параллельны) и записать канонические уравнения прямой не представляется возможным.
Задача 12. Написать канонические уравнения прямой.
Канонические уравнения прямой:
,
где 
– координаты какой-либо точки прямой, 
– ее направляющий вектор.
Найдем какую-либо точку прямой 
. Пусть , тогда
Следовательно, 
– координаты точки, принадлежащей прямой.
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку "Решить". Теоретическую часть и численные примеры смотрите ниже.
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α 1 и α 2:
Поскольку векторы n 1 и n 2 коллинеарны, то существует такое число λ ≠0, что выполнено равенство n 1 =λ n 2 , т.е. A 1 =λ A 2 , B 1 =λ B 2 , C 1 =λ C 2 .
Умножив уравнение (2) на λ , получим:
Если выполненио равенство D 1 =λ D 2 , то плоскости α 1 и α 2 совпадают, если же D 1 ≠λ D 2 то плоскости α 1 и α 2 параллельны, то есть не пересекаются.
2. Нормальные векторы n 1 и n 2 плоскостей α 1 и α 2 не коллинеарны (Рис.2).
Если векторы n 1 и n 2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
где x 0 , y 0 , z 0 , m, p, l действительные числа, а t − переменная.
Равенство (5) можно записать в следующем виде:
Пример 1. Найти линию пересечения плоскостей α 1 и α 2:
| α 1: x +2y +z +54=0. | (7) |
Решим систему линейных уравнений (9) отностительно x, y, z . Для решения системы, построим расширенную матрицу:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a 22 . Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
Получим решение:
Получили уравнение линии пересечения плоскостей α 1 и α 2 в параметрическом виде. Запишем ее в каноническом виде.
Ответ. Уравнение линии пересечения плоскостей α 1 и α 2 имеет вид:
| (15) |
α 1 имеет нормальный вектор n 1 ={A 1 , B 1 , C 1 }={1, 2, 7}. Плоскость α 2 имеет нормальный вектор n 2 ={A 2 , B 2 , C 2 }={2, 4, 14}.
n 1 и n 2 коллинеарны (n 1 можно получить умножением n 2 на число 1/2), то плоскости α 1 и α 2 параллельны или совпадают.
α 2 умножив на число 1/2:
| (18) |
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α 1 имеет нормальный вектор n 1 ={A 1 , B 1 , C 1 }={5, −2, 3}. Плоскость α 2 имеет нормальный вектор n 2 ={A 2 , B 2 , C 2 }={15, −6, 9}.
Поскольку направляющие векторы n 1 и n 2 коллинеарны (n 1 можно получить умножением n 2 на число 1/3), то плоскости α 1 и α 2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α 2 умножив на число 1/3:
| (19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α 1 и α 2 совпадают.
Пусть в канонических уравнениях прямой
коэффициент отличен от нуля, т. е. прямая не параллельна плоскости хОу. Запишем эти уравнения раздельно в таком виде:
При нашем условии уравнения (6) вполне определяют прямую. Каждое из них в отдельности выражает плоскость, причем первая из них параллельна оси Оу, а вторая - оси
Таким образом, представляя прямую линию уравнениями вида (6), мы рассматриваем ее как пересечение двух плоскостей, проектирующих эту прямую на плоскости координат xOz и yOz. Первое из уравнений (6), рассматриваемое в плоскости определяет проекцию данной прямой линии на эту плоскость; точно так же второе из уравнений (6), рассматриваемое в плоскости определяет проекцию данной прямой линии на плоскости yOz. Итак, можно сказать, что дать уравнения прямой линии в виде (6) - это значит дать ее проекции на плоскости координат хOz и yOz.
Если бы направляющий коэффициент был ранен нулю, то обязательно хотя бы один из двух других коэффициентов, например , был бы отличен от нуля, т. е. прямая не была бы параллельна плоскости yOz. В этом случае мы могли бы выразить прямую
уравнениями плоскостей, проектирующих ее на координатные плоскости записав уравнения (5) в виде
Таким образом, любая прямая может быть выражена уравнениями двух плоскостей, проходящих через нее и проектирующих ее на координатные плоскости. Но определять прямую совсем не обязательно именно такой парой плоскостей.
Через каждую прямую проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно, представляют собой уравнения этой прямой.
Вообще всякие две не параллельные между собой плоскости с общими уравнениями
определяют прямую их пересечения.
Уравнения (7), рассматриваемые совместно, называются общими уравнениями прямой.
От общих уравнений прямой (7) можно перейти к ее каноническим уравнениям. Для этой цели мы должны знать какую-нибудь точку прямой и направляющий вектор.
Координаты точки легко найдем из данной системы уравнений, выбирая одну из координат произвольно и решая после этого систему двух уравнений втносителыю оставшихся двух координат.
Для отыскания направляющего вектора прямой заметим, что этот вектор, направленный по линии пересечения данных плоскостей, должен быть перпендикулярным к обоим нормальным векторам этих плоскостей. Обратно, всякий вектор, перпендикулярный к параллелен обеим плоскостям, а следовательно, и данной прямой.
Но векторное произведение также обладает этим свойством. Поэтому за направляющий вектор прямой можно принять векторное произведение нормальных векторов данных плоскостей.
Пример 1. Привести к каноническому виду уравнения прямой
Выберем произвольно одну из координат. Пусть, иапример, . Тогда
откуда Итак, мы нашли точку (2, 0, 1), лежащую на прямой,
Находя теперь векторное произведение векторов получаем направляющий вектор прямой Поэтому канонические уравнения будут:
Замечание. От общих уравнений прямой вида (7) можно перейти к каноническим, и не прибегая к векторному методу.
Предварительно остановимся несколько подробнее на уравнениях
Выразим из них х и у через . Тогда получим:
где положено
Уравнения (6) называются уравнениями прямой в проекциях на плоскости
Установим геометрический смысл постоянных М и N: М представляет собой угловой коэффициент проекции данной прямой на плоскость координат (тангенс угла этой проекции с осью Oz), а N есть угловой коэффициент проекции данной прямой на плоскость координат (тангенс угла этой проекции с осью Oz). Таким образом, числа определяют направления проекций данной прямой линии на две плоскости координат, а значит, они характеризуют и направление самой данной прямой. Поэтому числа М и N называют угловыми коэффициентами данной прямой.
Чтобы выяснить геометрический смысл постоянных положим в уравнениях (6) прямой линии тогда получим: т. е. точка лежит на данной прямой. Очевидно, эта точка есть точка пересечения данной прямой с плоскостью Итак, суть координаты следа данной прямой линии на плоскости координат
Теперь легко сделать переход от уравнений в проекциях к каноническим. Пусть, например, даны уравнения (6). Решая эти уравнения относительно , найдем:
откуда непосредственно получаем канонические уравнения в виде
Пример 2. Привести канонические уравнения прямой
к уравнениям в проекциях на плоскости
Данные уравнения переписываем в виде
Решая первое из этих уравнений относительно х, а второе относительно у, найдем искомые уравнения в проекциях:
Пример 3. Привести уравнения в ппоекциях
к каноническому виду.
Решая данные уравнения относительно , получим.